九九は九九でも割り算九九。江戸からの贈物。

数ある掛図の中でも現代人が最も頭を捻るのが、この除算九九図でしょう。九九と言えば掛け算の乗算九九しか思い及ばず、インド式二桁掛け算に驚いているようでは、祖先の知恵に対して失礼というもの。ぜひ、頭に汗かいてこの掛図と格闘してみてください。

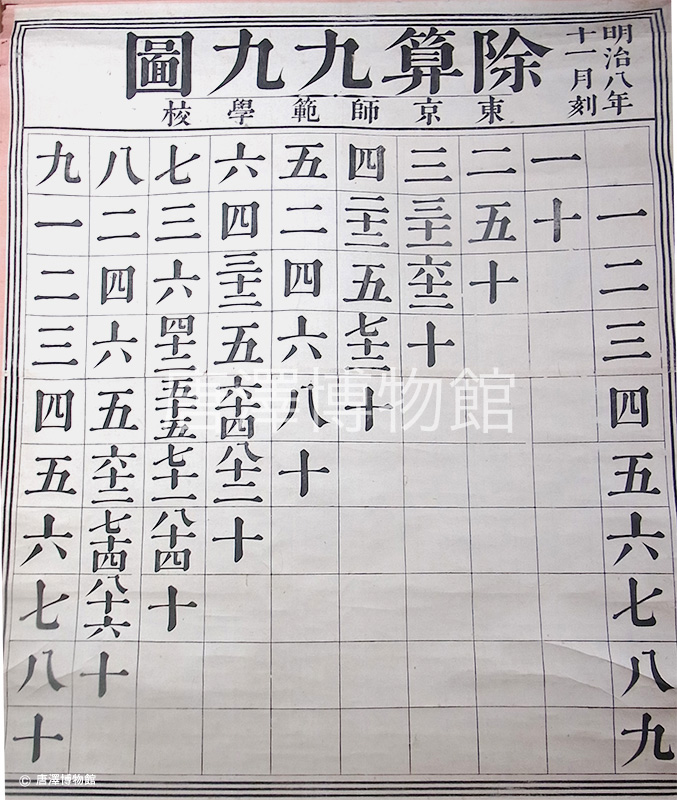
明治９年発行の『師範学校改正小学教授方法』によれば、「右の行の一より九までを上の段の一より九までにて割る時は其下に書たる数となる　其読法は上の一を以て右の行の一を割る時は次の行の十分となる　又上の段の二にて右の行の一を割る時は五分となる　其下の二も三も同じ理にて三を五つにすれば六分となるが如し　日本算なれば（二一天作ノ五）（三一三十ノ一）（四一二十ノ二）（五一加一）と呼ぶ是なり」とあります。

つまり、上の段の１～９は除数（割る数）、縦の１～９は被除数（割られる数）、交わったところの数字（基本、商と余りです）を暗記するわけですが、これは算盤を使って割り算計算するときに暗誦した割声（わりごえ）「八算」を明治８年東京師範学校が表にしたものなのです。和算の往来物（教科書）で江戸期のベストセラー数学書『塵劫記（じんこうき）』には、必ずこの八算が記載されており、江戸の人が割り算計算する際の必須アイテムでした。

『小学教授方法』に日本算と記されているのがこの八算のことで、「二一天作の五」つまり、二でもって一を割ると五分になる、という意味の割声は少し前まで多くの日本人の知るところでした。ちなみに進退窮まった時に使う「二進(にっち)も三進(さっち)もいかない」という言い回しも、八算の２でも３でも割り切れない、というところからきています。

一度この表を暗記すれば、除数が１桁なら指が自然と動いて珠算が出来るようになります。

例えば１２３４５÷３の場合

まず「三一三十ノ一」（万の位の１を３で割る）と唱えながら、万の位を３に直し、千の位の２に余り１を加えると次のようになります。

次に、「三進が一十」（千の位の３を３で割る）、千の位の３から３を引き０にして、万の位に１を足します。

そして、「三進が一十」（百の位の３を３で割る）で同様に百の位についても３を０にして、千の位に１を足します。

それから、十の位の４を３と１に分けて計算します。「三進が一十」（十の位の４のうち３を３で割る）で十の位から3を引いて百の位に1を足すとこのようになり、

「三一三十ノ一」（十の位の残り１を３で割る）で、十の位の１を３に直し、一の位の５に１を足すと、次のようになります。

さらに、一の位の６を３と３に分けて考え、「三進が一十」（一の位の６のうち３を３で割る）でこのようになり

「三進が一十」（一の位の残り３を３で割る）で一の位の３から３を引いて０にして、十の位に１を足します。

つまり、答えは４１１５となるわけです。声に出しながら玉をはじいていくとなかなか気持ちが良いものです。

明治５年頒布された『学制』には「算術九九数位加減乗除　但洋法ヲ用フ」とあり、算術は洋法即ち筆算（暗算・珠算ではなく、数字を書いて計算すること）を教えるように指示していますが、江戸期から受け継がれた珠算の便利さは文明開化も何のその、どっこい生き残ったわけです。