学と術は、あたかも二本の糸のようであり、それぞれの糸には個々の学や術が連なっている。これが前回読んだくだりで述べられた譬えでした。その話の最後で、西先生はこんなことを言っています。

今世上學術の多寡を論せんには、學を爲すものは少く術をなすものは多し。従來學術相關して、學あれは其術あるか如く並ひ行くものにあらす。

（「百學連環」第50段落第第14文～第15文）

訳してみます。

現在の学術の多寡を論ずるなら、学をなすものは少なく、術をなすものが多い。従来から学術は、互いに関連しあって、学があればそれに関する術があるといった具合に〔同じぐらい〕並んであるものではない。

つまり、学に対して術が並列して揃っているわけではない、という次第です。多少ということで言えば、学は少なく、術が多いというのですね。現在はどうなっているでしょうか。西先生の頃に比べて、学も相当に細分化されている印象がありますが、実際のところは分かりません。そもそも「学」や「術」をどのように区別したり、数えるかというやり方次第という面もありそうです。

ともあれ、ここでの含意は、学と術が必ず対応して揃っているとは限らないということで理解しておけばよいでしょう。

続きを読んで参りましょう。学術に焦点を当てたまま、いよいよ最後の話題へと転じてゆきます。

又學術に二ツの性質あり。一は common 一は particular 是なり。普通とは一理の萬事に係はるを云ひ、殊別とは唯タ一事に關するを云ふなり。譬へは算術の如きは今日の萬事より其他種々に關渉す、是普通なり。本草學の如き是を殊別とす。又窮理學の如きは殊別にして、歴史、算術、地理學の如きは是學問の普通の性質、即ち今日學ふ所の普通なり。此の普通、殊別の二ツは學ひ行く所に就て論するにあらす。今學ひ行くには時あり、處あり、人あるものなれは、世に普通學と稱するなとは〔他の〕人より其人を指して云ふ語にして、學の性質に就て論するにあらす。是等も亦區別して了解せさるへからす。

（「百學連環」第50段落第第16文～第24文）

common には「普通」、particular には「殊別」という漢語が、左側に添えてあります。訳してみましょう。

また、学術には二つの性質がある。一つは「普通（common）」、もう一つは「個別（particular）」である。「普通」とは、一理が万事に関わることを指す。「個別」とは、一事だけに関わることをいう。例えば、算術は、今日のあらゆること、その他さまざまなことに関わっている。つまり、算術は普通〔の学〕である。植物学は個別である。また、物理学も個別だ。歴史、算術、地理学は、学問に普通〔共通〕の性質を備えるものであり、今日学ぶものとしては普通のものだ。ただし、この「普通」「個別」という二つの区別は、学びについて論じたものではない〔ことに注意しよう〕。なにかを学ぼうと思えば、いつ、どこで、誰に学ぶかということが関わってくるものだ。世間で「普通学」と称しているものは、余人がある人を指して言う言葉であって、学そのものの性質について論じているわけではない。こうしたこともまた区別して理解する必要がある。

さて、ここでは「百学連環」全体の構造に関わる大きな話が登場します。つまり、学術全体を大きく二分する性質が論じられています。その二つの性質について西先生は、common を「普通」、particular を「殊別」と訳しました。

これを現代語としてなんと訳すかは、おおいに迷うところです。というのも、現在「普通」といえば、たいていは「ありふれているもの」といった意味で使われることのほうが多いように思います。「どこにでもいる普通の高校生」式の用法ですね。しかし、ここではその意味ではありません。「一理が万事に関わる」というわけですから、「普（あまね）く通じる」という意味です。

気持ちとしては「普遍」「一般」「共通」とでも訳したいところですが、「普通」としておきました。西先生が注意しているように、当時使われていた「普通学」という言葉との重なり具合も見えるようにしておきたいと考えてのことです。ですから、分かりづらいと感じる向きは「普遍学」「一般学」「共通学」などと読み替えていただければと思います。また、particular のほうは、「個別」や「特殊」と言い換えてよいでしょう。

このくだりの余白には、次のような図が掲げられています。

向かって上の図は、一つの理が万事に対応していることを示したものだと思われます。つまり「普通」を表しているのでしょう。対する下の図は、一つの理が一事に対応していること、つまり「個別」を示しています。といっても、この図では一つの理が横棒に対応しているようにも見えますね。乙本で同じ図を見ると、この点が訂正されているようです。

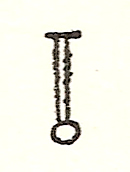
このように、一理から出た縦線は、短い横線に対応するように正されていますね。

さらに面白いのは、その具体例です。西先生がここで挙げているものを、改めて分けて書くとこうなります。

普通　歴史、算術、地理学
個別　植物学、物理学

私は、初めてここを読んだとき、「あれ？」と不思議に思いました。というのも、自分の感覚では、どちらかというと物理学は普通学で、むしろ歴史や地理学こそ個別学のように感じたからです。この疑問については、次回もう少し詳しく検討してみることにします。

ここではあともう一点、世間でいう「普通学」と混同してはいけないという注意について見ておきましょう。世間で言われている「普通学」とは、おそらく、いまで言う「一般教養」を指していると思われます。例えば、「百学連環」講義からは少し後のものになりますが、元良勇次郎（1858-1912）の『教育新論』（中近堂、1884）の第2章に「普通学ト専門学ノ関係」という議論が出ています。現代でも、教養科目と専門科目といった区別は残っていますね。

あるいは、木村知治『帝国議会衆議院撰挙人心得』（兎屋、1889）には、議員が備えるべきものとして学識が挙げられています。そこでは「普通の学識を有したるもの」である必要ありと論じられ、「普通学」とは何かという解説が施されていたりもします。そればかりか「普通学を充分修めたる人物にあらざれば如何に理屈を構ふるも徒に空論に陥り或は偏理となり……」と、専門学だけ学ぶのでは駄目だと釘を刺していたりします。

西先生が、「世に普通學と稱するなとは〔他の〕人より其人を指して云ふ語」と言ったものも、「普通の学識を有す」という場合のように、人に属するものとしての学のことを指していたのだろうと思います。しかし、「百学連環」で言う「普通学／個別学」という区別は、そうではなく、学術そのものを分類するものの見方であるというわけです。

次回は、「百学連環」における学術分類の全体を見渡しながら、「普通学」と「個別学」の違いについて、さらに検討してみることにしましょう。

*

歴＝歷（U+6B77）
即＝卽（U+537D）