第16回で、進級試験に合格することがいかに大変か、在籍比率を例にお話しましたが、はたしてその試験はどのようなものだったのでしょうか。『師範学校　小学試験成規』（明治８年）の中から一部、ご紹介しましょう。

この本は、東京師範学校を明治７年６月に卒業し、神奈川県師範学校教員となった小林義則が、下等小学の試験法と例題を記したものです。明治７年の段階では、近代的な教授法を学んだ東京師範学校卒業生は小林を含めわずか３７名しかおらず、江戸期以来の旧来の教育関係者が講習所に通い、にわか教師として雇用されていました。規則に定められた進級試験の仕方にも戸惑う教師が多い中、小林が一つの指針として自ら執筆、出版したと考えられます。

凡例によれば各級の科目と配点は、次の通りです。算術２０点、読物・摘書（てきしょ）２０点、講義１０点、書取（第五級からは作文に変更）２０点、問答１５点、習字１５点。評価は減点方式ですが、作文と習字はそれぞれ４段階評価（甲２０点、乙１５点、丙１０点、丁５点）と３段階評価（大佳１５点、佳々１０点、佳５点）です。１００点満点で、５０点以上が及第とされています。答えは記されていませんので、以下の答えは私の試算、私見です。

まず、算術問題から。第八級（小学１年前期）は以下の４問です。（１）～（３）は漢数字を算用数字に、算用数字を漢数字になおす問題、（４）は暗算問題です。

（１）七十七　（２）九十　（３）６９　（４）６＋５＋４＋２＋７＋５＝

これは簡単なので答えは割愛しますが、漢数字を常用していた日本人が算用数字を学ぶには、教師も生徒もだいぶ苦労し、「１は一の倒立」「３はだるま」などと言いつつ覚えたそうです。第七級（小学１年後期）では、ローマ数字「CLXXII」を算用数字になおす問題が出題されています。現代では時計の文字盤ぐらいでしか馴染みがありませんが、当時は漢数字、算用数字と並び、ローマ数字も学んでいました。ちなみにCが１００、Lが５０、Xが１０を表すので、答えは１７２となります。

第六級（小学２年前期）以上は、筆算２問、文章問題１問、暗算１問の構成ですが、第一級（小学４年後期）ともなると筆算もかなり複雑です。

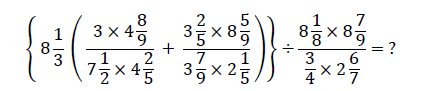
ずいぶん込み入った「分数ぶんの分数」問題で、解くには根気が必要ですが、ぜひ挑戦してみてください。答えは文末に記します。

読物・摘書は、合わせて２０点。読物は学習した掛図や教科書の中から指示された範囲を朗読します。摘書は、黒板に抜き書きされた単語の読み方を口頭で答え、○が付いたものはその意味も述べます。各級かなりの難問揃いですが、例えば第三級（小学３年後期）は以下の８問です。

（１）峠　（２）纔　（３）○磽确　（４）○職分田　（５）香美　（６）律令　（７）藺席　（８）甲奴

難しい漢字がありますが、「纔」は「わず（か）」もしくは「ひたた」、「磽确」は「こうかく」、「藺席」はイ草で作られた筵（むしろ） のことで「いむしろ」と読むと思われます。○の付いた「磽确」は石の多いやせた土地、「職分田」（しきぶんでん） は、律令制で官職に支給した田のこと、などと言葉の意味を説明しなくてはいけません。「香美」と「甲奴」は地名で、それぞれ高知県の「かみ」、広島県の「こうぬ」のことです。明治の小学生はこんな難しい言葉を勉強していたのですね。

講義は、読物で朗読した部分の内容を簡潔に説明します。正しければ１０点、一つ間違えるごとに第八級は２点半、それより上の級では５点ずつ引かれます。

★

算術の答え・・・７１００/７１８９