帰納法と真理についての議論が続きます。具体例として、前回の政治学を筆頭に、諸学術における真理の例が登場します。この畳みかけるようなくだり、少し長くなりますが、区切らずまとめて読んでみましょう。

格物學の眞理の一ツは地球の引力なり。器械學の一ツの眞理は車の囘轉する必す輪に避心力あるか如く、天文學の一ツの眞理は星の囘轉するものは必す囘轉し、恒星は幾星ありても運轉させる如く、化學の一ツの眞理は均一の量なり。こは equivalent とて其元素の同しきなり。譬えは鐵に酸素の和する必す赤き錆生し、銅に和する緑色を生するか如き、其酸素の和する必す元トありて、一匁和するか、或は二匁或は三匁と、其元の變して一匁五分なとゝ和するの理なし。地質學の一ツの眞理は地球の中心カラニーッテンより上向の地膚に至るまて幾層の層なりありて、土は土、石炭は石炭、石は石と◎の如く何處にても其層り同しきものなり。又 Pneumatics 卽ち氣學の眞理は何處にても上へなれは上へほと地上よりは空氣の層り少くなるなり。算術の眞理は二二か四の如く、何國にても二ツか二ツ集まれは四となるなり。幾何學の一ツの眞理は直線の二線十字に横切るときは如何しても角度を生するなり。是皆眞理の一ツにして、大略此の如きものなり。故に學たるものは苟も無二の眞理を捕へて胸中に深く知らさるへからす。

（「百学連環」第39段落第30文～第39文）

上記のうち「錆」には「サビ」とルビが振られています。では、訳してみます。

物理学の真理の一つは地球の引力である。器械学〔力学〕の一つの真理は、車が回転する場合には必ず遠心力が生じるということ。天文学の一つの真理は星の回転するものは必ず回転すること、恒星はどれだけあっても〔見かけの上では〕運行しないということ。化学における一つの真理は均一の量ということだ。これは「当量（equivalent）」というもので、元素〔が過不足なく反応する物質の量〕が同じであることを指す。例えば、鉄に酸素が化合すると必ず赤い錆が生じ、銅に化合すると緑青が生ずるように、〔ある物質が〕酸素と化合する単位というものが必ずある。つまり、1グラム化合するか、2グラム、あるいは3グラムかであって、その単位が変化して1.5グラムなどと化合することはない。地質学における一つの真理は、地球の中心〔カラニーッテン〕より上の地殻に至るまで何層もあり、土は土、石炭は石炭、石は石と◎のように、どの場所でもその重なり方は同じということである。また、気体学（Pneumatics）における真理は、どこにおいても高くなればなるほど、地上と比べて空気の層が薄くなるということだ。算術の真理は、2×2=4（ににんがし）のように、国を問わず二つが二つ集まれば四つとなるという次第。幾何学の一つの真理は、二つの直線が交わる場合、必ず角度が生じるということである。これらはいずれも真理の一つであり、おおまかには以上のようなことだ。つまり、学というものは、まことに無二の真理を捉えて、心中で深く知るということに他ならないのである。

まず、訳文について、いくつか補足しておきましょう。現代語訳では、「匁」を「グラム」と置き換えました。本来であれば、1匁＝約3.75グラムですが、ここでは厳密な数値ではなく、整数比になることがポイントなので、敢えてこのようにしています。

また、地質学のところに現れる「カラニーッテン」なる言葉については、以前から分からずにいたのですが、今回も推測がつかずにおります。まずこれは何語なのかというところから始まって、地質学の用語なのかそうでないのか、各種言語の辞書や当時の地質学の書物などをひっくり返してあれこれ調べてはいるのですが、浅学の悲しいところ、これだという解釈に手が届いておりません。

後に真相が分かってから笑われるのを承知で申せば、ここは日本語として読むべきところなのではないかと目下は考えています。その理由や、他にどんな可能性を考えたかという話をすれば、それこそちょっとした笑いの種を提供できると思いますが、ここでの講義内容からすれば本質的なことではないので別の機会に譲ります。いずれにしても、「百学連環」講義ノートの原本を見る機会に恵まれたら、真っ先に確認したい箇所の一つであります。

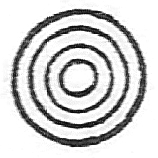
それから、これは原文と訳文の双方に対して、もう一点補足です。文中で「◎」と記した箇所は、上のような図が文字のように挿入されているところです。層が同心円状に重なっているような図ですね。

さて、いかがでしょうか。登場した学術を並べてみると、以下の通りです。

物理学
器械学〔力学〕
天文学
化学
地質学
気体学
算術
幾何学

ご覧のように八つの学問分野が並んでいます。これらの学術は、いずれもこの「百学連環」講義の本論で、それぞれについてもう少し詳しく論じられるものです（ただし、「地質学」については、西先生の「覚書」はあれど、講義記録には見えません）。

また、一見些末なことかもしれませんが、この並び順は、西先生が「百学連環」の本論で諸学術を説明してゆく順序にかなり似ています。「物理学」から「気体学」までの並び順は、「気体学」を「器械学」の後ろに入れれば、講義本編の順序と重なります。この並び順にどのような意味があるのかということも気になるところですが、それについてはこの「総論」精読の最後に考えてみたいと念じております。

それぞれの「真理」の例は、ご覧の通りの内容で、現代でも中高生ぐらいまでの課程で教えられる知識に類することではないかと思います。つまり、それだけ基礎的で重要なことであります。これは想像に過ぎませんが、これだけの「真理」を矢継ぎ早に列挙してみせる西先生の口吻に接して、聴講者たちは圧倒されたのではないでしょうか。なにしろ、自ら進んで学んだりその機会を得た人は別として、当時の多くの日本の人にとって、こうした西洋の新知識は目新しいものだったでありましょうから。

このくだりが興味深いのは、前回読んだ政治学の例を除くと、ほとんどが現在で言うところの「理系」の学問であることです。これは、西先生が「百学連環」において学問全体を分類する際の「心理上学」と「物理上学」という分類で言えば、後者に該当します（数学は、これとは別の分類が施されています）。なぜ物理上学の例が多いのか、いささか気になるところです。

また、こうした「真理」の例は、ここでの本題である「帰納法」と、どのような関係にあるのでしょうか。これらの「真理」は、帰納法によって発見されたということなのでしょうか。いまのところは、まだはっきりと明示されてはいません。

第90回「リンゴと万有引力」の末尾でも述べたように、以前のトピックに比べて、この「帰納法」に関する議論では、たいへん多くの言葉が費やされています。講義の一つの山場と言ってよいでしょう。というわけで、先ほどの疑問を念頭に置きながら、先を見てみることにします。